基于Wi-Fi CSI的摔倒检测(二):CSI数据预处理之离散小波变换
1小波变换的特点及适用性
相较于传统去噪声方法,小波去噪的原理简单,计算速度快。因为有离散小波变换的快速计算方法。所以在这种实时性要求较高的检测系统中更适合使用。由于小波变换的基函数是有尺度区分的,所以其时域和频域分辨率都是可调的,根据使用者对信号分析的要求进行参数的选择和调节。从性能上来说小波去噪很好的保留了信号的原始特征,在滤除噪声后能很好地凸显信号的特征方便后续提取摔倒信息。
2小波变换的原理以及步骤:
有很多种基于小波变换的去噪方法。本节我们主要讲两种去噪方法:
1 重构法
2非线性小波变换阈值法
小波变换去噪:小波变换将原始信号分解为低频和高频分量,然后将高频系数设为0,然后反变换,恢复去噪后的信号。
3具体实现以及效果
1、基于非线性小波变换软阈值法
小波去噪[xd,cxd,lxd]=wden(x,tptr,sorh,scal,n,'wname')
式中:输入参数x 为需要去噪的信号;
tptr :阈值选择标准.
1)无偏似然估计(rigrsure)原则。它是一种基于史坦无偏似然估计(二次方程)原理的自适应阈值选择。对于一个给定的阈值t,得到它的似然估计,再将似然t 最小化,就得到了所选的阈值,它是一种软件阈值估计器。
(2)固定阈值(sqtwolog)原则。固定阈值thr2 的计算公式为:thr 2log(n) 2 = (6)式中,n 为信号x(k)的长度。
(3)启发式阈值(heursure)原则。它是rigrsure原则和sqtwolog 原则的折中。如果信噪比很小,按rigrsure 原则处理的信号噪声较大,这时采用sqtwolog原则。
(4)极值阈值(minimaxi)原则。它采用极大极小原理选择阈值,产生一个最小均方误差的极值,而不是没有误差。2.sorh :阈值函数选择方式,即软阈值(s) 或硬阈值(h).
scal :阈值处理随噪声水平的变化,scal=one 表示不随噪声水平变化,scal=sln 表示根据第一层小波分解的噪声水平估计进行调整,scal=mln 表示根据每一层小波分解的噪声水平估计进行调整.
n 和wname 表示利用名为wname 的小波对信号进行n 层分解。
输出去噪后的数据xd 及xd 的附加小波分解结构[cxd,lxd].
经过对比测试我们在本信号中发现。
参数设置为 'heursure','s','one',10,'sym3' 效果最好。
效果:我们先随机选取一根天线的载波进行观察:
如图为第二根天线第30跟载波的降噪效果:
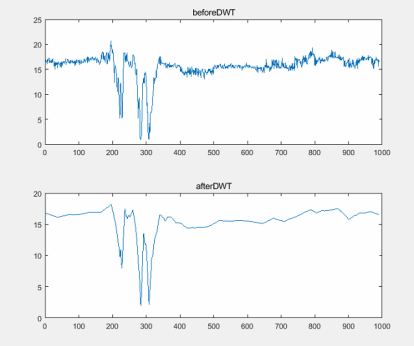
代码如下:
clear all
clc
csi_trace = read_bf_file('sample_data/logfallr111.dat');
pac_nEm=size(csi_trace,1);
subcarrier=zeros(1,990);
Hall=zeros(990,30);
Z=zeros(990,30);
Zk=zeros(990,1);
for j=30
%·分别按照时间顺序导入第j个子载波的990个值 for i=1:990;
csi_entry=csi_trace{i};
csi=get_scaled_csi(csi_entry);
csi1=squeeze(csi(1,:,:)).';% 30*3 complex
csiabs=db(abs(csi1));
csiabs=csiabs(:,2);
csi1=csi1(:,2);
subcarrier(i)=csiabs(j);% %10子载波幅度
if(subcarrier(i)>=35)
subcarrier(i)=35;
else if(subcarrier(i)<=1)
subcarrier(i)=1;
end
end
end
% %第j个子载波滤波yd=wden(subcarrier,'heursure','s','one',10,'sym3');
vs=movvar(yd,50)
figure(1)
subplot(2,1,1);
plot(subcarrier);
title('beforeDWT');
subplot(2,1,2);
plot(yd);
title('afterDWT');
figure(2)
plot(vs);
xlabel('time(s)');
ylabel('variance');
title('movvar_Origin');
hold on
Hall(:,j)=yd.';
end若将30个载波放在一起进行对比则更加明显的发现高频杂波被滤除掉。
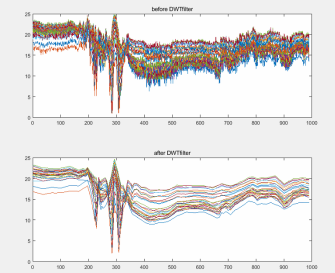
如果将分解级数降低到3级我们可以发现更多的高频噪声被包含进来;与此同时分解层数继续提高例如22级分解则效果并不明显:
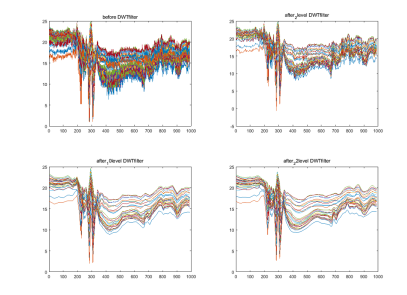
代码如下:
clear all
clc
csi_trace = read_bf_file('sample_data/logfallr111.dat');
pac_nEm=size(csi_trace,1);
subcarrier=zeros(1,990);
Hall=zeros(990,30);
Z=zeros(990,30);
Zk=zeros(990,1);
for j=1:30
%分别按照时间顺序导入第j个子载波的990个值 for i=1:990;
csi_entry=csi_trace{i};
csi=get_scaled_csi(csi_entry);
csi1=squeeze(csi(1,:,:)).';% 30*3 complex
csiabs=db(abs(csi1));
csiabs=csiabs(:,2);
csi1=csi1(:,2);
subcarrier(i)=csiabs(j);% 10子载波幅度
if(subcarrier(i)>=35)
subcarrier(i)=35;
else if(subcarrier(i)<=1)
subcarrier(i)=1;
end
end
end
% %第j个子载波滤波
yd=wden(subcarrier,'heursure','s','one',10,'sym3');
subplot(2,1,1)
plot(subcarrier);
title('before DWTfilter');
hold on
subplot(2,1,2);
plot(yd);
title('after DWTfilter');
hold on
Hall(:,j)=yd.';
end分解层次不同的对比部分代码:
yd=wden(subcarrier,'heursure','s','one',2,'sym3');
yd1=wden(subcarrier,'heursure','s','one',10,'sym3');
yd2=wden(subcarrier,'heursure','s','one',22,'sym5');
subplot(2,2,1)
plot(subcarrier);
title('before DWTfilter');
hold on
subplot(2,2,2);
plot(yd);
title('after_2level_ DWTfilter');
hold on
subplot(2,2,3);
plot(yd1);
title('after_10level_ DWTfilter');
hold on
subplot(2,2,4);
plot(yd2);
title('after_22level_ DWTfilter');
hold on(2)使用重构法进行去噪,直接提取小波变换后最后一层的近似系数来提取图像的特征。
代码如下:
clc
clear all
warning('off')
csi_trace = read_bf_file('sample_data/logfalls11.dat');
subcarrier=zeros(3,990,30);
for k=1:3
for j=1:30
for i=1:990
csi_entry = csi_trace{i};%依次读各组数据包,为了平均
csi = get_scaled_csi(csi_entry);
csi=csi(1,:,:);%1*3*30
csi1=squeeze(csi).';% 30*3 complex
csiabs=db(abs(csi1));%30*3 double%判断该矩阵维数size(),中最小值是否为1,不是得话要选择一组作为有效值
csiabs=csiabs(:,k);
csi1=csi1(:,k);
subcarrier(k,i,j)=csiabs(j);%j子载波幅度
if(subcarrier(k,i,j)>=35)
subcarrier3(k,i,j)=35;
else if(subcarrier(k,i,j)<=1)
subcarrier(k,i,j)=1;
end
end
end
end
end
y=subcarrier;
subcarrier1=subcarrier(2,:,17); %选择某个具体载波
X=subcarrier1';
figure(1)
subplot(2,1,1);
plot(X);
%通过db5小波基进行6尺度小波分解
[c,l]=wavedec(X,6,'db5');
a1=appcoef(c,l,'db5',1);
a2=appcoef(c,l,'db5',2);
a3=appcoef(c,l,'db5',3);
a4=appcoef(c,l,'db5',4);
a5=appcoef(c,l,'db5',5);
a6=appcoef(c,l,'db5',6);
figure(3);
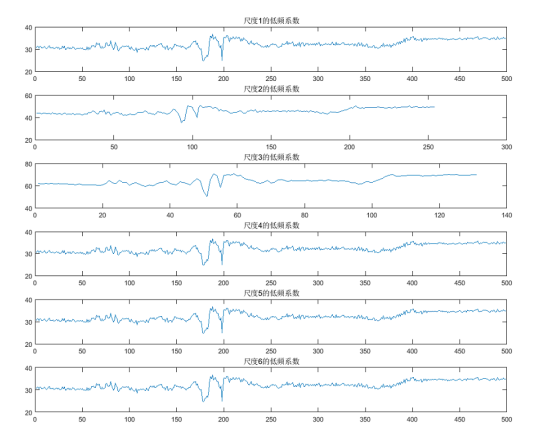
subplot(6,1,1);plot(a1);title('尺度1的低频系数');
subplot(6,1,2);plot(a2);title('尺度2的低频系数');
subplot(6,1,3);plot(a3);title('尺度3的低频系数');
subplot(6,1,4);plot(a1);title('尺度4的低频系数');
subplot(6,1,5);plot(a1);title('尺度5的低频系数');
subplot(6,1,6);plot(a1);title('尺度6的低频系数');
%
d1=detcoef(c,l,1);
d2=detcoef(c,l,2);
d3=detcoef(c,l,3);
d4=detcoef(c,l,4);
d5=detcoef(c,l,5);
d6=detcoef(c,l,6);
figure(4);
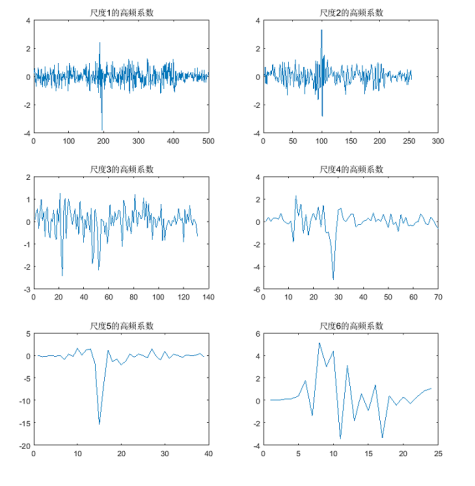
subplot(3,2,1);plot(d1);title('尺度1的高频系数');
subplot(3,2,2);plot(d2);title('尺度2的高频系数');
subplot(3,2,3);plot(d3);title('尺度3的高频系数');
subplot(3,2,4);plot(d4);title('尺度4的高频系数');
subplot(3,2,5);plot(d5);title('尺度5的高频系数');
subplot(3,2,6);plot(d6);title('尺度6的高频系数');
d6=zeros(1,length(d6));
d5=zeros(1,length(d5));
d4=zeros(1,length(d4));
d3=zeros(1,length(d3));
d2=zeros(1,length(d2));
d1=zeros(1,length(d1));
%
a1=a1';
a5=a5';
d1=d1';
d2=d2';
d3=d3';
d4=d4';
d5=d5';
d6=d6';
cA5=appcoef(c,l,'db5',5);
A5=wrcoef('a',c,l,'db5',5);
figure(1);
subplot(2,1,2),
plot(A5);
hold on
title('重构信号');结果如下:
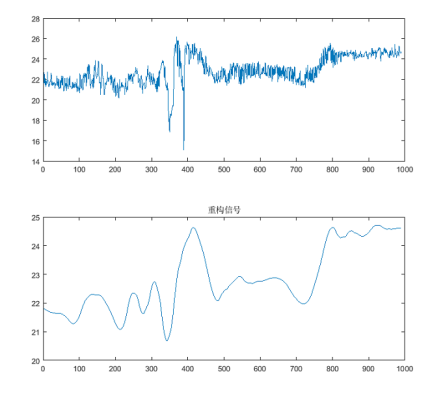
- 分享
- 举报
-
浏览量:17852次2020-12-21 18:20:26
-
浏览量:14470次2020-12-19 14:41:57
-
浏览量:25637次2021-01-08 11:33:04
-
浏览量:30462次2020-12-18 00:01:24
-
浏览量:15938次2021-01-08 01:48:55
-
浏览量:13035次2021-01-08 03:03:13
-
浏览量:8799次2021-01-08 01:26:48
-
2023-01-13 11:33:00
-
浏览量:601次2023-12-25 14:11:19
-
浏览量:2014次2019-09-16 14:33:10
-
浏览量:195次2023-12-14 16:51:13
-
浏览量:1021次2023-01-29 11:28:01
-
浏览量:3355次2022-02-18 09:00:16
-
浏览量:1166次2020-02-27 09:14:10
-
浏览量:5871次2021-01-08 02:27:20
-
浏览量:1581次2020-01-13 10:31:14
-
浏览量:6313次2020-06-05 15:50:07
-
浏览量:140次2024-01-17 15:30:26
-
浏览量:111次2024-03-01 16:56:38
-
广告/SPAM
-
恶意灌水
-
违规内容
-
文不对题
-
重复发帖
技术凯





 微信支付
微信支付举报类型
- 内容涉黄/赌/毒
- 内容侵权/抄袭
- 政治相关
- 涉嫌广告
- 侮辱谩骂
- 其他
详细说明


 微信扫码分享
微信扫码分享 QQ好友
QQ好友








好