模式识别之数据降维（六）：LDA方法介绍与实现_专栏

一、LDA的基本原理

之前的文章中，我们已经介绍了PCA，它在进行数据降维时，不考虑分类的情况，是利用数据自身进行特征提取的一种方法。这就使得PCA经常用于数据的降燥而不是数据的分类任务中。本篇文章要介绍的LDA方法，在进行特征提取时，将学习数据的标签信息也考虑在内，使得分类时的准确率大大增加。
LDA（Linear Discriminant Analysis），即线性判别分析。它的基本原理可以用一句话概括：将数据投影变换，使得相同类别数据之间的距离最小，不同类别数据之间的距离最大，简称：类间距离最大，类内距离最小。我们可以用一张图进行解释：

这张图大家已经很熟悉了，我们可以把蓝色的“X”和红色的“O”看作两类数据，在投影之后，我们可以看出，相同类别之间的距离很小，不同类别之间的距离很大。以上就是LDA的基本思想。那么这个类间距离和类内距离如何表示呢？数学家们已经为我们提供了相关公式了，如下所示：
（1）类内距离公式：

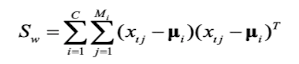
其中，C为类别个数，比如：二分类任务时，C=2.，xij为第i类的第j个数据，ui为第i类样本的均值。
（2）类间距离公式：

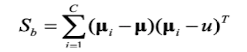
其中，ui为第i类样本的均值，u的计算公式如下：

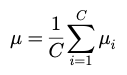
我们最终的目的，就是要让类间距离最小，类内距离最大，我们可以设定一个判别式：

判别式最大时，我们的LDA达到最优

二、进行LDA的步骤

计算数据的均值，类内离散度（类内距离）和类间离散度（类间距离）
计算判别矩阵J的特征值以及特征向量

和之前PCA算法一样，我们对特征向量进行排列，最终选择一定数量的特征向量，特征向量的数量即为选择特征的个数，经过推导，选择的最大特征数i等于类别数C-1。最终得到变换矩阵，降维的过程实际上是将原数据经过变换矩阵变换到新的数据：

LDA的步骤如上，具体涉及到复杂的数学推导，本文不再赘述，感兴趣的读者可以自行查阅资料。

三、LDA的Matlab实现

与PCA分析不同的是，LDA分析用到了数据的标签信息。所以，在进行二分类和多分类的降维操作时，要分开处理。在处理二分类数据时，最大的投影维度为1维。在处理多分类数据时，最大的投影维度为C-1维。
（1）先导入二分类数据，计算均值和内类离散度矩阵

%LDA
clear
% 先使用二分类数据进行LDA
load('2-Class Problem.mat');
tic
train_num1=size(Training_class1,2);
train_num2=size(Training_class2,2);
d=size(Training_class1,1);
% 计算均值
miu_1=mean(Training_class1,2);
miu_2=mean(Training_class2,2);
miu=(miu_1+miu_2)/2;
% 计算类内离散度矩阵
s_w1=(Training_class1-miu_1)*(Training_class1-miu_1)';
s_w2=(Training_class2-miu_2)*(Training_class2-miu_2)';
s_w=s_w1+s_w2;

（2）计算类间离散度矩阵，的特征值以及特征向量。并对特征值进行排列

% 计算类间离散度矩阵
s_b=(miu_1-miu_2)*(miu_1-miu_2)';
% 计算特征值和特征向量
[u,lamda]=eig(s_w\s_b);
lamda=ones(1,d)*lamda;%eig函数生成的特征值转换成行向量
% 将特征值和特征向量合成一个矩阵，第一列为特征值，从第二列开始为特征向量，特征向量按行排列
lamda_u=[lamda;u];
lamda_u=lamda_u';
lamda_u=sortrows(lamda_u,1,'descend');%对特征向量按lamda大小进行降序排列
lamda=lamda_u(:,1);%分离特征值
u=lamda_u(:,2:end);%分离特征向量

（3）求解变换矩阵，并保存

k=1;%提取的特征数为1,对于二分类问题，最大的投影维度为1维
u=u(1:k,:);
u_2_class=u;
%保存提取的特征向量
save('feature_LDA','u_2_class');

（4）读取多分类数据集

% 使用多分类数据进行LDA
load('Mult-class Problem.mat');
% 获取类别数
class_nums=Label_training(end);
% 训练数据量
train_num=size(Training_data,2);

（5）计算均值、类内离散度矩阵

% 计算均值、类内离散度矩阵
for i=1:class_nums
miu_i(:,i)=mean(Training_data(:,Label_training==i),2);%均值
%第i类类内离散度矩阵
s=0;
for j=1:train_num
    s=s+(Training_data(:,Label_training==i)-miu_i(:,i))*(Training_data(:,Label_training==i)-miu_i(:,i))';
end
s_w_i(:,:,i)=s;
end
miu=mean(miu_i,2);
s_w=sum(s_w_i,3);

（6）计算类间离散度矩阵，的特征值以及特征矩阵，并对特征向量，并对特征向量按特征值降序排列。

% 计算类间离散度
s_b=(miu_i-miu)*(miu_i-miu)';
% 计算特征值和特征向量
[u,lamda]=eig(inv(s_w)*s_b);
lamda=ones(1,d)*lamda;%eig函数生成的特征值转换成行向量
%将特征值和特征向量合成一个矩阵，第一列为特征值，从第二列开始为特征向量，特征向量按行排列
lamda_u=[lamda;u];
lamda_u=lamda_u';
lamda_u=sortrows(lamda_u,1,'descend');%对特征向量按lamda大小进行降序排列
lamda=lamda_u(:,1);%分离特征值
u=lamda_u(:,2:end);%分离特征向量

（7）计算变换矩阵，并保存

k=16;%提取的最大特征数为c-1=16
u=u(1:k,:);
u_mult_class=u;
%保存提取的特征向量
save('feature_LDA','u_mult_class','-append');  
toc

完整代码如下：

%LDA
clear
% 先使用二分类数据进行LDA
load('2-Class Problem.mat');
tic
train_num1=size(Training_class1,2);
train_num2=size(Training_class2,2);
d=size(Training_class1,1);
% 计算均值
miu_1=mean(Training_class1,2);
miu_2=mean(Training_class2,2);
miu=(miu_1+miu_2)/2;
% 计算类内离散度矩阵
s_w1=(Training_class1-miu_1)*(Training_class1-miu_1)';
s_w2=(Training_class2-miu_2)*(Training_class2-miu_2)';
s_w=s_w1+s_w2;
% 计算类间离散度矩阵
s_b=(miu_1-miu_2)*(miu_1-miu_2)';
% 计算特征值和特征向量
[u,lamda]=eig(s_w\s_b);
lamda=ones(1,d)*lamda;%eig函数生成的特征值转换成行向量
% 将特征值和特征向量合成一个矩阵，第一列为特征值，从第二列开始为特征向量，特征向量按行排列
lamda_u=[lamda;u];
lamda_u=lamda_u';
lamda_u=sortrows(lamda_u,1,'descend');%对特征向量按lamda大小进行降序排列
lamda=lamda_u(:,1);%分离特征值
u=lamda_u(:,2:end);%分离特征向量
k=1;%提取的特征数为1,对于二分类问题，最大的投影维度为1维
u=u(1:k,:);
u_2_class=u;
%保存提取的特征向量
save('feature_LDA','u_2_class');  
% 使用多分类数据进行LDA
load('Mult-class Problem.mat');
% 获取类别数
class_nums=Label_training(end);
% 训练数据量
train_num=size(Training_data,2);  
% 计算均值、类内离散度矩阵
for i=1:class_nums
miu_i(:,i)=mean(Training_data(:,Label_training==i),2);%均值
%第i类类内离散度矩阵
s=0;
for j=1:train_num
    s=s+(Training_data(:,Label_training==i)-miu_i(:,i))*(Training_data(:,Label_training==i)-miu_i(:,i))';
end
s_w_i(:,:,i)=s;
end
miu=mean(miu_i,2);
s_w=sum(s_w_i,3);
% 计算类间离散度
s_b=(miu_i-miu)*(miu_i-miu)';
% 计算特征值和特征向量
[u,lamda]=eig(inv(s_w)*s_b);
lamda=ones(1,d)*lamda;%eig函数生成的特征值转换成行向量
%将特征值和特征向量合成一个矩阵，第一列为特征值，从第二列开始为特征向量，特征向量按行排列
lamda_u=[lamda;u];
lamda_u=lamda_u';
lamda_u=sortrows(lamda_u,1,'descend');%对特征向量按lamda大小进行降序排列
lamda=lamda_u(:,1);%分离特征值
u=lamda_u(:,2:end);%分离特征向量
k=16;%提取的最大特征数为c-1=16
u=u(1:k,:);
u_mult_class=u;
%保存提取的特征向量
save('feature_LDA','u_mult_class','-append');  
toc

程序运行结果：

四、LDA的二分类测试

下面，我们将测试使用LDA降维后的数据的分类效果。二分类测试数据和测试算法与PCA及以前的测试相同。先对数据利用LDA生成的变换矩阵进行降维，然后使用贝叶斯算法进行分类，观察正确率和程序运行时间。
完整代码如下：

%LDA性能测试--二分类,学习算法采用贝叶斯
clear
load('2-Class Problem.mat');
load('feature_LDA')
tic
n1=size(Training_class1,2);
n2=size(Training_class2,2);
% 特征提取
Training_class1_b=u_2_class*Training_class1;
Training_class2_b=u_2_class*Training_class2;
Testing_b=u_2_class*Testing;
% 先验概率
pw1=n1/(n1+n2);
pw2=n2/(n1+n2);
[miu1,sigma1]=ParamerEstimation(Training_class1_b);
[miu2,sigma2]=ParamerEstimation(Training_class2_b);
predict_label=0;
[b,n]=size(Testing_b);
for i=1:n
x=Testing_b(:,i);
pxw1=gaussian(miu1,sigma1,x);
pxw2=gaussian(miu2,sigma2,x);
if pw1*pxw1>pw2*pxw2
    predict_label(i)=1;
else
    predict_label(i)=2;
end
end
% 计算精度
acc=sum(predict_label==Label_Testing)/n;
toc
fprintf('正确率是%.2f%%\n',acc*100);

程序运行结果：

二分类最终降到一维，也可以达到100%的正确分类，时间只用了0.01s

五、多分类测试

同二分类，先进行降维，然后进行贝叶斯多分类。使用的数据集也与之前的算法测试数据集一致
完整代码如下：

%PCA主成分分析性能测试--多分类,学习算法采用贝叶斯
clear
load('Mult-class Problem.mat');
load('feature_LDA')
tic
% 特征提取
u=u_mult_class;
Training_data=u*Training_data;
Testing_data=u*Testing_data;
% 获取类别数
class_nums=Label_training(end);
% 获取数据集大小
test_nums=size(Testing_data,2);
train_nums=size(Training_data,2);    

Training_temp=0;
predict=0;

for class=1:class_nums
    [miu(:,class),sigma(:,:,class)]=ParamerEstimation(Training_data(:,Label_training==class));
    num=size(Training_data(:,Label_training==class),2);
    % 计算先验概率
    pw(class)=num/train_nums;
end
for i=1:test_nums
    for class=1:class_nums
        % 计算类的条件概率
        pxw(class)=gaussian(miu(:,class),sigma(:,:,class),Testing_data(:,i));
        % 计算判别式
        g_x(class)=log(pw(class))+log(pxw(class));
    end
    [~,argmax]=max(g_x);
    predict(i)=argmax;
    if mod(i,100) == 0
        acc=sum(predict==Label_testing(1:i))/(i);
        disp(['预测数据号：' num2str(i)])
        disp(['准确度是：' num2str(acc)])
    end
end
% 计算正确率         
acc=sum(predict==Label_testing)/(test_nums);
toc
disp(['总准确度是：' num2str(acc)])

程序运行结果：

可以看到，由于使用了类别的标签信息，LDA降维后可以达到70%的正确率。况且只用了7s左右。