【深度学习】基于深度神经网络进行权重剪枝的算法（一）_专栏

【深度学习】基于深度神经网络进行权重剪枝的算法（一）

1 pruning
2 代码例子
3 tensorflow2 keras 权重剪裁（tensorflow-model-optimization）
    3.1 第一步 安装优化包
    3.2 Train a model without pruning
    3.3 Fine-tune pre-trained model with pruning(目前只支持序列模型和函数式模型，尚未支持子类化模型 )
    3.4 剪裁前后模型对比
    3.5 对比评估裁剪前后的模型
    3.6 训练一个剪枝的模型
4 应用

1 pruning

参数：权重和偏差
系数：权重
如何定义”不重要的权重“呢？文中说了一个经典的例子：
这个函数有两个系数：1和5。

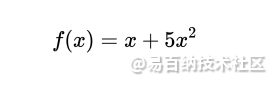
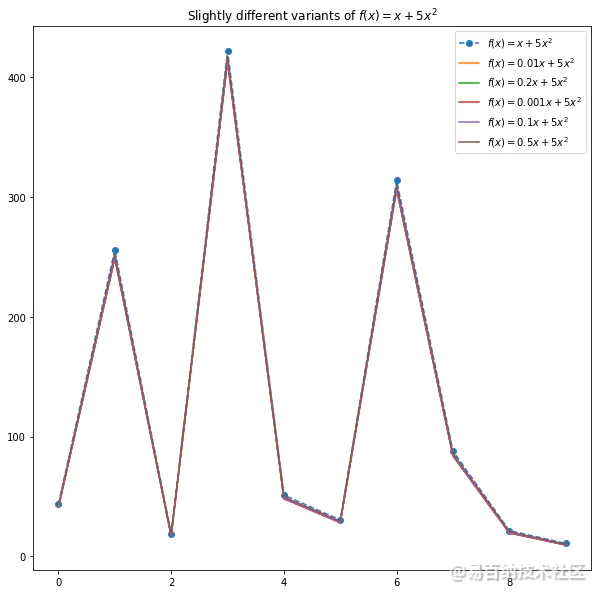
在这里插入图片描述
当我们改变第一个系数1时，函数图像只会发生微小的改变。(如图1) 因此这个系数可以看作”不重要的系数“。丢弃这样的系数不会严重影响函数的表现。

在这里插入图片描述
神经网络中的应用
如何定义神经网络中的不重要的权重呢？
分析梯度下降（gradient descent）中的优化过程（optimization）。所有的权重都用相同的梯度量级（gradient maginitudes）进行更新。损失函数的梯度与权重（和偏差）有关。在优化过程中，有的权重比其他权重用更大的幅度量级（有正有负）进行更新，这些权重可以看作”更重要“的权重。
（个人理解：大权重幅度会导致input经过该权重后变化更大）
训练结束之后，我们检查网络每一层的权重幅值，并找出”重要“的权重。寻找方法如下（heuristics）：
（1）降序排列权重幅值
（2）找到在队列中更早出现的那些幅值（对应weight maginitudes更大）”那些“具体有多少，取决于有百分之多少的权重需要被剪枝。（percentage of weights to be pruned）
（3）设定一个阈值，权重幅值在阈值之上的权重会被视为是重要的权重。这个阈值的设定也有以下几种方法：
（a）这个阈值可以是整个网络中最小的权重梯度
（b）这个阈值可以是该网络中某一层的最小权重阈值。在这种情况下，不同层的“重要”权重之间是有偏差的。

2 代码例子

下面我们在MNIST数据集上来讨论这些概念。我们使用一个浅的全连接层网络，该网络的拓扑结构如下：
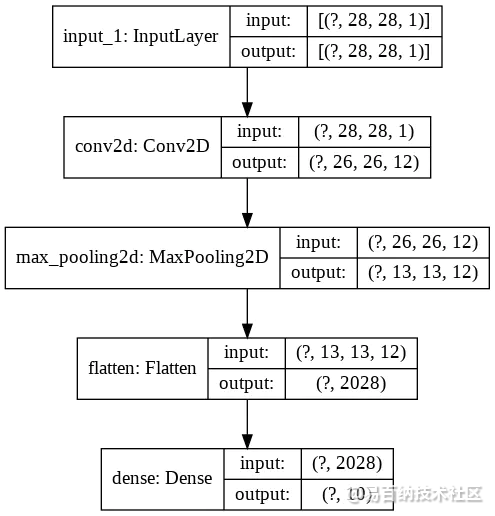
在这里插入图片描述
这个网络一共有20410个可训练的
参数，训练该网络10个epoch就可以得到一个好的baseline。

下面我们对这个网络进行剪枝，我们用到tensorflow里的tensorflow_model_optimization函数，这个函数给我们提供了两种剪枝技巧：
拿一个训练好的网络，剪枝并且再训练
随机初始化一个网络，从头开始剪枝和训练
我们拿来了之前训练好的网络，然后我们需要有一个pruning schedule，同时在训练过程中保证sparsity level constant （即每一层固定为0的权重数目占总数目的百分比）以下代码完成了上述任务：

pruning_schedule = tfmot.sparsity.keras.ConstantSparsity(
          target_sparsity=target_sparsity,
          begin_step=begin_step,
          end_step=end_step,
          frequency=frequency
)

pruned_model = tfmot.sparsity.keras.prune_low_magnitude(
    trained_model, pruning_schedule=pruning_schedule
)

一个被剪枝过的模型在再次重新训练之前需要重新编译（re-compile）。以下代码进行了编译和打印。

pruned_model.compile(loss='sparse_categorical_crossentropy',
    optimizer='adam',
    metrics=['accuracy'])
pruned_model.summary()

Layer (type)                 Output Shape              Param #   
=================================================================
prune_low_magnitude_conv2d ( (None, 26, 26, 12)        230       
_________________________________________________________________
prune_low_magnitude_max_pool (None, 13, 13, 12)        1         
_________________________________________________________________
prune_low_magnitude_flatten  (None, 2028)              1         
_________________________________________________________________
prune_low_magnitude_dense (P (None, 10)                40572     
=================================================================
Total params: 40,804
Trainable params: 20,410
Non-trainable params: 20,394

我们发现参数的数目有变化。这是因为tfmot对网络里每一个被剪枝的权重加了一个 non-trainable mask。这个mask的值为0或1。
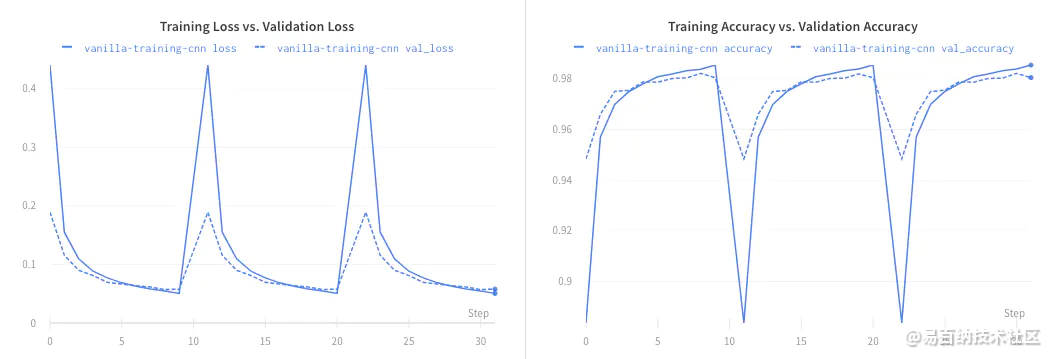
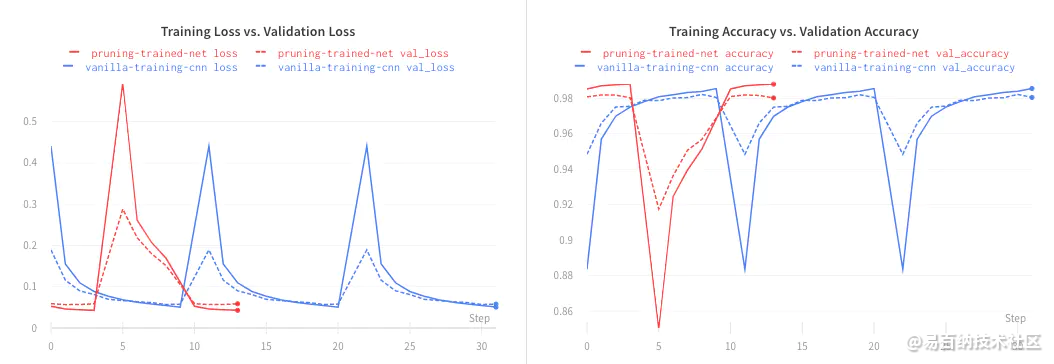
下面是训练结果。红色线对应剪枝实验。从训练结果中我们发现，剪枝并不影响模型表现。
在这里插入图片描述

3 tensorflow2 keras 权重剪裁（tensorflow-model-optimization）

剪枝原理较为简单，简单理解，即在训练过程中，在迭代一定次数后，便对net中的接近0的权重，都置为0，已达到对模型剪枝的作用，以此反复，直到net的参数达到目标的稀疏度。这样，模型训练完成后，模型里面大多数的weight皆为0，那么，当我们使用zip进行压缩时，模型便可以得到很大程度的压缩，且在推断过程中，减少了很多的计算量。

3.1 第一步安装优化包

 pip install -q tensorflow-model-optimization

3.2 Train a model without pruning

正常训练一个特定任务的模型

import tensorflow as tf
from tensorflow import keras
mnist = keras.datasets.mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

# 归一化预处理数据，即将数据转换为（0，1）的范围.
train_images = train_images / 255.0
test_images = test_images / 255.0

# 定义模型结构
model = keras.Sequential([
  keras.layers.InputLayer(input_shape=(28, 28)),
  keras.layers.Reshape(target_shape=(28, 28, 1)),
  keras.layers.Conv2D(filters=12, kernel_size=(3, 3), activation='relu'),
  keras.layers.MaxPooling2D(pool_size=(2, 2)),
  keras.layers.Flatten(),
  keras.layers.Dense(10)
])

# 编译模型，SparseCategoricalCrossentropy是交叉熵函数，是标签是非one-hot编码下使用的
#如果标签是one-hot编码，需要使用CategoricalCrossentropy
model.compile(optimizer='adam',
              loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
              metrics=['accuracy'])
#训练模型
model.fit(
  train_images,
  train_labels,
  epochs=4,
  validation_split=0.1,
)

model_result = model.evaluate(test_images,test_labels,verbose=0)
print(model_result)

# 输出[0.06889190595522524, 0.9784]

#保存模型
_, keras_file = tempfile.mkstemp('.h5',dir='./')
tf.keras.models.save_model(model, keras_file, include_optimizer=False)
print('Saved baseline model to:', keras_file)

3.3 Fine-tune pre-trained model with pruning(目前只支持序列模型和函数式模型，尚未支持子类化模型 )

import tensorflow_model_optimization as tfmot

prune_low_magnitude = tfmot.sparsity.keras.prune_low_magnitude

# Compute end step to finish pruning after 2 epochs.
batch_size = 128
epochs = 2
validation_split = 0.1 # 10% of training set will be used for validation set. 

num_images = train_images.shape[0] * (1 - validation_split)
end_step = np.ceil(num_images / batch_size).astype(np.int32) * epochs

# Define model for pruning.
pruning_params = {
      'pruning_schedule': tfmot.sparsity.keras.PolynomialDecay(initial_sparsity=0.50,
                                                               final_sparsity=0.80,
                                                               begin_step=0,
                                                               end_step=end_step)
}

model_for_pruning = prune_low_magnitude(model, **pruning_params)

# `prune_low_magnitude` requires a recompile.
model_for_pruning.compile(optimizer='adam',
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
              metrics=['accuracy'])

model_for_pruning.summary()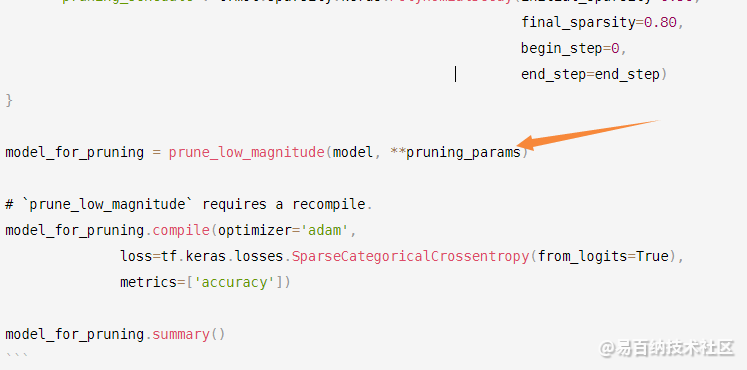

在这里插入图片描述
黄色箭头对模型进行剪枝，得到新的模型后重新编译。
使用keras构建深度学习模型，我们会通过model.summary()输出模型各层的参数状况，如下：

________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_4 (Dense)              (None, 7)                 35        
_________________________________________________________________
activation_4 (Activation)    (None, 7)                 0         
_________________________________________________________________
dense_5 (Dense)              (None, 13)                104       
_________________________________________________________________
activation_5 (Activation)    (None, 13)                0         
_________________________________________________________________
dense_6 (Dense)              (None, 5)                 70        
_________________________________________________________________
activation_6 (Activation)    (None, 5)                 0         
=================================================================
Total params: 209
Trainable params: 209
Non-trainable params: 0
_________________________________________________________________

3.4 剪裁前后模型对比

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
reshape_1 (Reshape)          (None, 28, 28, 1)         0         
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 26, 26, 12)        120       
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 13, 13, 12)        0         
_________________________________________________________________
flatten_1 (Flatten)          (None, 2028)              0         
_________________________________________________________________
dense_1 (Dense)              (None, 10)                20290     
=================================================================
Total params: 20,410
Trainable params: 20,410
Non-trainable params: 0

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
prune_low_magnitude_reshape_ (None, 28, 28, 1)         1         
_________________________________________________________________
prune_low_magnitude_conv2d_1 (None, 26, 26, 12)        230       
_________________________________________________________________
prune_low_magnitude_max_pool (None, 13, 13, 12)        1         
_________________________________________________________________
prune_low_magnitude_flatten_ (None, 2028)              1         
_________________________________________________________________
prune_low_magnitude_dense_1  (None, 10)                40572     
=================================================================
Total params: 40,805
Trainable params: 20,410
Non-trainable params: 20,395

通过对比，发现经过剪枝后的参数量多了Non-trainable params: 20,395，即多了20395个不可训练的参数。是tensorflow-model-optimization为网络中的每个权重添加的不可训练掩码，表示是否要修剪该权重，掩码为0或1。在修剪完模型后，我们需要使用strip_pruning来删除暂时添加的这些Non-trainable params。

3.5 对比评估裁剪前后的模型

logdir = tempfile.mkdtemp()

callbacks = [
  tfmot.sparsity.keras.UpdatePruningStep(),
  tfmot.sparsity.keras.PruningSummaries(log_dir=logdir),
]

model_for_pruning.fit(train_images, train_labels,
                  batch_size=batch_size, epochs=epochs, validation_split=validation_split,
                  callbacks=callbacks)

Train on 54000 samples, validate on 6000 samples
Epoch 1/2
54000/54000 [==============================] - 9s 164us/sample - loss: 0.0869 - accuracy: 0.9768 - val_loss: 0.1107 - val_accuracy: 0.9690
Epoch 2/2
54000/54000 [==============================] - 8s 143us/sample - loss: 0.0973 - accuracy: 0.9733 - val_loss: 0.0851 - val_accuracy: 0.9747

UpdatePruningStep回调，使其在训练过程中处理修剪更新。
PruningSummaries提供用于跟踪进度和调试的日志。

3.6 训练一个剪枝的模型

tensorflow提供一个prune_low_magnitude()的API来训练模型，模型中会移除一些连接。基于Keras的API可以应用于独立的网络层，或者整个网络。在高层级，此技术是在给定规划和目标稀疏度的前提下，通过迭代的移除(即zeroing out)网络层之间的连接。

例如，典型的配置是目标稀疏度为75%，通过每迭代100步(epoch)裁剪一些连接，从第2000步(epoch)开始。更多配置需要查看官方文档。

4 应用

在这里插入图片描述

《Second order derivatives for network pruning: Optimal Brain Surgeon》中：
为了改进泛化，简化网络，减少硬件或存储需求，提高进一步训练的速度，我们研究了利用误差函数的所有二阶导数来进行网络剪枝(即，从训练的网络中删除不重要的权值)。在某些情况下，可以提取规则。
基于损失函数相对于权重的二阶导数（对权重向量来说即Hessian矩阵）来衡量网络中权重的重要程度，然后对其进行裁剪。
。第二种思路就是考虑参数裁剪对loss的影响。其实前面提到的始祖级的OBD和OBS就是属于此类。但这两种方法需要计算Hessian矩阵或其近似比较费时。近年来有一些基于该思路的方法被研究和提出。如2016年论文《Pruning Convolutional Neural Networks for Resource Efficient Transfer Learning》也是基于Taylor expansion，但采用的是目标函数相对于activation的展开式中一阶项的绝对值作为pruning的criteria。这样就避免了二阶项（即Hessian矩阵）的计算。2018年论文《SNIP: Single-shot Network Pruning based on Connection Sensitivity》将归一化的目标函数相对于参数的导数绝对值作为重要性的衡量指标。