【剖析】傅里叶变换、拉普拉斯变换、Z变换(二）)

【剖析】傅里叶变换、拉普拉斯变换、Z变换

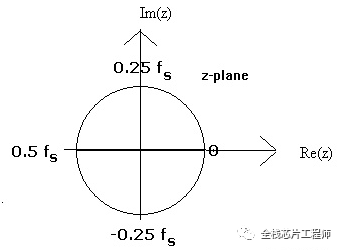
接着上文聊，我们知道在s域上，虚轴上不同的点对应不同的频率，而z域上单位圆与s域虚轴对应，可见，z域单位圆上不同的点，代表了不同的频率。

对于z域的传递函数的零极点，也有和s域零极点类似的结论：

• 规律1：如果在单位圆上有零点，则在零点所对应的频率上幅值响应为零；
• 规律2：对于不在单位圆上的零点，在单位圆上离零点最近的点对应的频率上幅值响应最小。
• 规律3：对于在单位圆内部的极点，在单位圆上离极点最近的点对应的频率上幅值响应最大。
• 规律4：如果极点和零点重合，对系统的频率响应没有影响。

单位圆逆时针从0 -> -0.5fs -> 0？

细心的朋友发现没？上图单位圆为何逆时针是从0->0.5fs，然后又从-0.5fs到0？耐心等待下文的解释。

很久以前，我们需要处理的信号只有模拟信号。但是现在我们步入了新时代——数字时代，大部分信号都变成数字式了，典型的数字信号长成这个样子：

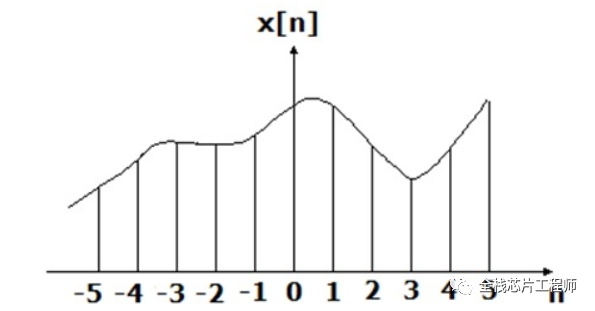
把模拟信号变成数字信号的过程称之为采样。

采样频率定义为：

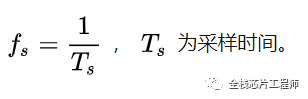
采样是一个有规律的周期性过程，也就说，采样会引入额外的谐波分量。举个简单的例子，现在有一个余弦信号，频率为 8Hz，表达式为：

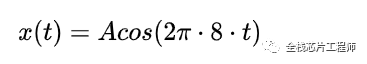
假设我们对这个余弦信号进行采样，采样频率fs为20MHz，采样结果如下图，其中虚线为原始信号，菱形为采样点的数值。

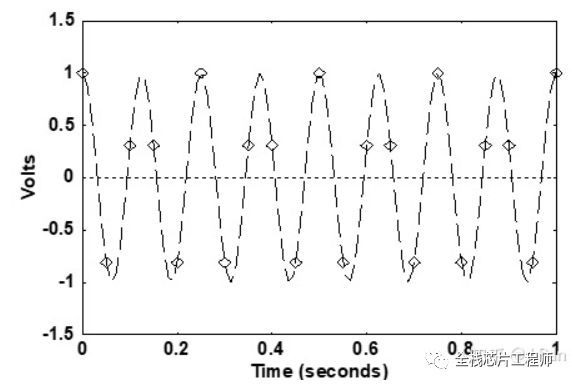
采样到的离散的点，我们用曲线拟合的方式即可恢复模拟信号，但是！

拟合出来的曲线可能是12Hz、28Hz，32Hz，48Hz，…，也就是说采样之后信号频谱有很多频率，而不单单是原信号频率8Hz。

为什么？怎么办？

采样定理

两个信号在时域相乘，在频域相当于卷积；在时域卷积，在频响相当于相乘。

狄拉克梳状函数（Dirac comb）

狄拉克函数定义为：

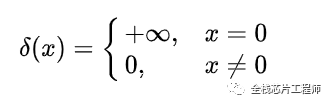
离散信号，其实就是连续信号f(t)与狄拉克梳状函数（也就是采样函数）的相乘，这就是采样。这是时域行为，在频域就是卷积！

狄拉克梳状函数无论在时域还是在频域，其形貌都是一系列的脉冲信号，感兴趣的朋友可以参考这个链接查看推导：https://zhuanlan.zhihu.com/p/45114376

举个例子：

对于余弦函数而言，比如：w=2πf, f=8Hz

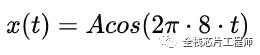
其傅里叶变换包含两个频率分量，分别是8Hz以及-8Hz，如下图：

采样频率fs为20Hz:

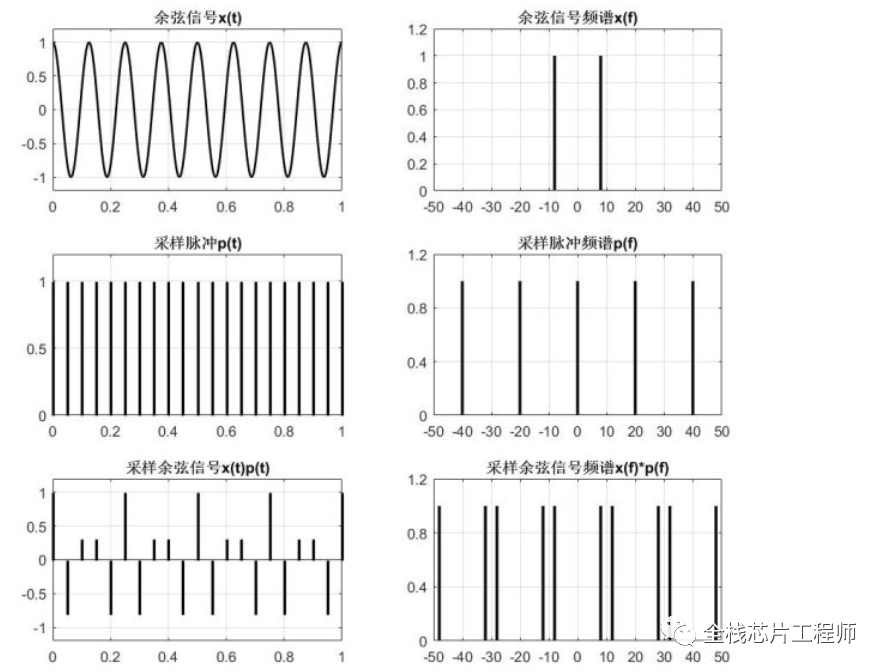
采样后的信号的频谱被周期延拓了，延拓的周期就是20Hz，也就是采样频率。

上文说了，对8Hz的余弦函数采样得到离散点，拟合出来的曲线可能是12Hz、28Hz，32Hz，48Hz，也就是说采样之后信号频谱有很多频率，而不单单是原信号频率8Hz。

现在明白了吧，12Hz是-8Hz平移一个采样周期(20Hz)得来的，28Hz是8Hz平移一个采样周期，32Hz是-8Hz平移两个采样周期，48Hz是8Hz平移两个采样周期。

得到了如下结论：对一个连续信号的采样，采样后的频谱相当于将采样前的频谱进行了延拓，延拓的周期就是采样频率。

奈奎斯特采样定律假设一个信号的频谱如下：

频谱中最大的频率为fmax ，用一个周期为fs的狄拉克梳状函数进行采样后的频谱为原频谱的周期延拓，示意图如下：

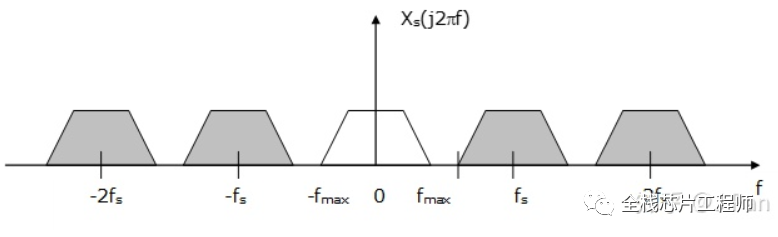
采样之后的频谱是一个周期函数，我们把[0, 1/2*fs]称为主值区间：

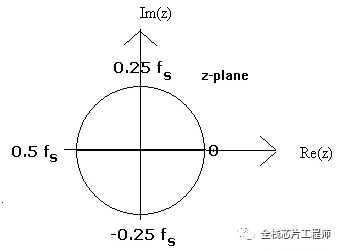
这就解释了上文的问题：细心的朋友发现没？上图单位圆为何逆时针是从0->0.5fs，然后又从-0.5fs到0？

接着思考下，如果采用频率小于信号最大频率的2倍：

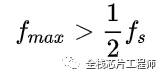
会发生原始频谱信号经过周期延拓后会有一部分重叠：

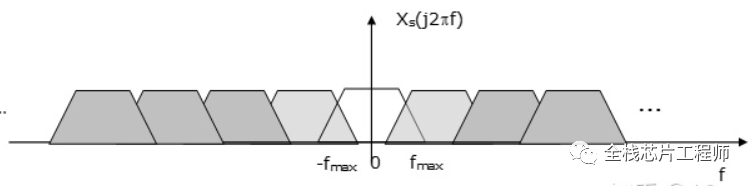
对于连续信号的进行抽样离散的话，必须保证采样频率是原连续信号最大频率分量的2倍频率以上，否则信号就难以复原。这就是采样定理，又叫奈奎斯特采样定理或香农采样定理。

零、极点影响频率响应

• 例子1：

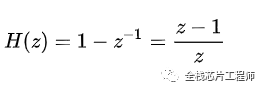
对于这个系统，在z=0有一个极点，在z=1时有一个零点。零、极点分布如下：

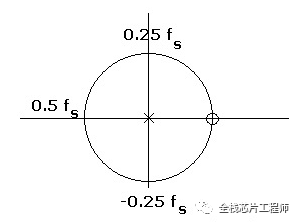
其中o表示零点，x表示极点。从z=1也就是单位圆上角度为零(也是频率为零)的点开始，此处z=1有一个零点，根据规律1，显然在频率为零时系统响应为零。

顺着单位圆沿逆时针方向旋转，我们离零点越来越远，零点的影响也越来越小，因此幅值响应会逐渐增大。当我们到达z=-1 ,也就是频率为1/2fs时，此时离零点最远，因此响应会达到一个最大值，当频率继续增大时，由于离零点又开始接近了，幅值响应又开始变小。

极点正好位于圆心位置，也就是说所有频率段离极点的距离都一样，因此可以认为都没影响。

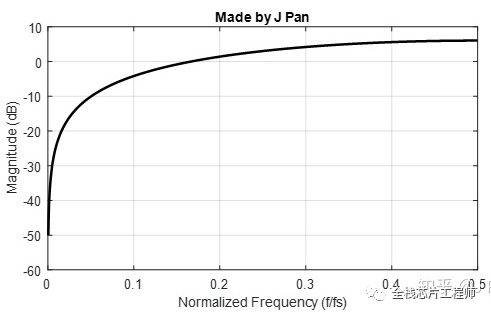
用freqz函数将系统的频响画出来，如下图，这个系统本质上是一个高通滤波器。

这个系统转换到时域：

是不是很惊喜，这本质就是一个差分，低频信号被过滤，高频信号通过。

• 例子2：

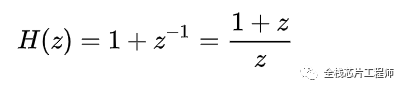
零极点图如下：

零点跑到了1/2*fs处，因此，系统的频响会先减小，到1/2*fs处达到最小值，然后又增加，具体频响如下图，这本质上是一个低通滤波器。

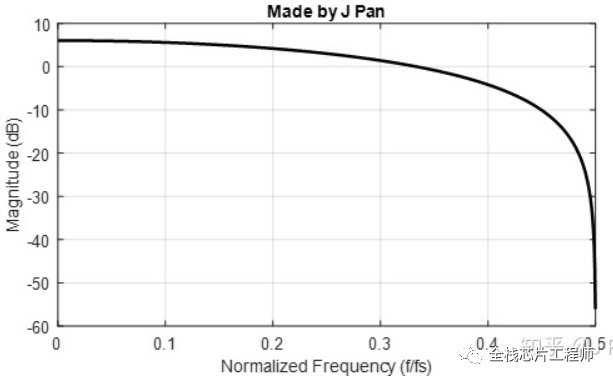
时域的表达式为：

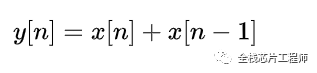
这本质就是一个离散求和，对应连续系统的积分，是一个低通滤波器。

低通、高通滤波有了，带阻呢？假如我们在0到1/2fs之间放置一个零点，那会不会是一个带阻滤波器呢？比如我们想在频率在3/8fs这个点的系统频率响应为零。

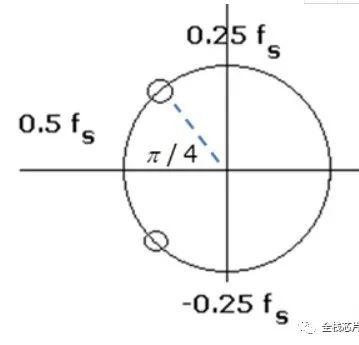
[0, 1/2*fs]称为主值区间，[-1/2*fs，0]为对称区间，因此，3/8fs处对应的相位角为3π/4，同时，-3π/4也是零点相位角。因此，传导函数为：

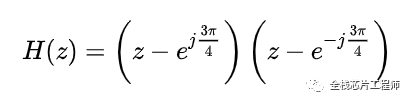
展开可得：

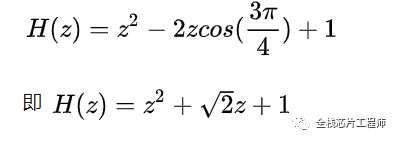
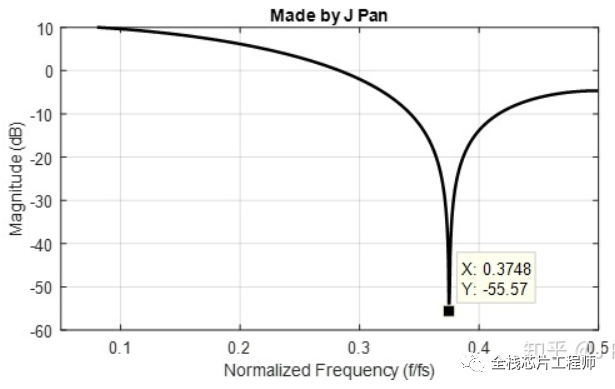
感兴趣的朋友继续推导下带通滤波器的设计，后面接着聊FIR、IIR滤波。

参考原文：

https://zhuanlan.zhihu.com/p/45138629

https://zhuanlan.zhihu.com/p/45114376

感谢阅读，别走！点赞、关注、转发后再走吧

转载：全栈芯片工程师